type
status
date
slug
summary
tags
category
icon
password
catalog
sort
在高并发场景中，频繁的浮点数转换（比如字符串和浮点数互转）可能成为性能瓶颈。比如日志解析、数据分析系统，每秒要处理上百万个浮点数字符串，转换效率直接影响系统吞吐量。
在算法工程中，一般关注四大核心维度：稳定、成本、效果、性能。
其中，性能尤为关键——它既能提升系统稳定性，又能降低成本、优化效果。因此，工程团队将微秒级的性能优化作为核心攻坚方向。
一、你每天都在用的浮点数，到底是个啥？
咱们先从一个生活场景说起：你打开手机计算器，输入"0.1+0.2"，结果显示0.30000000000000004。这时候你可能会纳闷：计算器是不是坏了？其实不是计算器的问题，而是浮点数在计算机里的"特殊脾气"导致的。
浮点数，简单说就是带小数点的数字，比如3.14、0.0001、-123.45。但计算机只认二进制（0和1），怎么把咱们熟悉的十进制小数变成二进制让机器看懂？又怎么把机器里的二进制数变回咱们能理解的十进制？这就是"浮点数转换"要解决的核心问题。
1.1 为啥需要浮点数？
你可能会想：整数用二进制表示挺简单的，小数为啥这么麻烦？因为现实世界的数值范围太广了——从微观世界的0.0000000001米，到宇宙尺度的1234567890123456789公里，要是用固定位数的二进制表示，要么精度不够，要么范围不够。
浮点数的思路跟科学计数法很像。比如1234.56可以写成1.23456×10³，这里的1.23456是"尾数"（有效数字），3是"指数"（决定小数点位置）。浮点数就是用二进制的科学计数法，把一个数拆成三部分：
- 符号位：0表示正数，1表示负数（跟正负号对应）
- 指数位：表示二进制的指数（决定数值的大小范围）
- 尾数位：表示二进制的有效数字（决定数值的精度）
三者的关系可以简单记为：数值 = (-1)^符号位 × 尾数 × 2^指数。
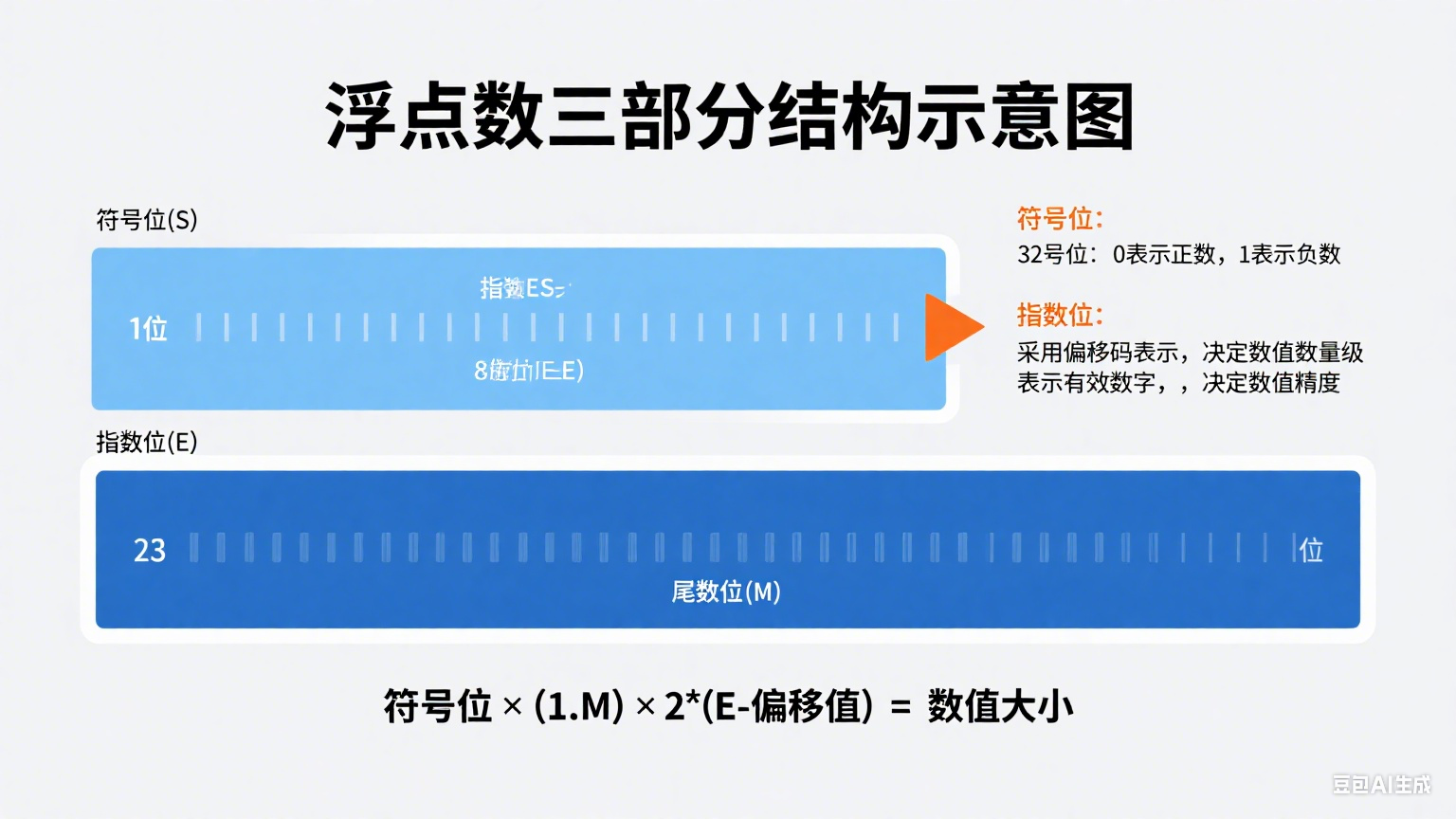
比如十进制的1.5，二进制是1.1，用浮点数表示就是：符号位0（正数），指数1（因为1.1×2⁰=1.1，实际指数计算需结合偏移值，后面细说），尾数1.1。
1.2 没有标准的日子有多乱？
在计算机发展早期，不同厂家对浮点数的表示没有统一规定。比如同一份数据，在IBM的机器上是3.14，到了DEC的机器上可能就变成了314，这给数据交换和程序移植带来了大麻烦。
想象一下：你在A电脑上写了个计算圆周率的程序，结果拿到B电脑上运行，得出的结果差了十万八千里——这可不是程序员的锅，而是浮点数格式不统一惹的祸。于是在1985年，IEEE（电气与电子工程师协会）站出来制定了一个标准，也就是咱们接下来要重点聊的IEEE 754标准。这个标准一出来，就像给浮点数定了"通用语言"，从此不同系统、不同硬件之间的浮点数交互终于有了统一的规矩。
二、IEEE 754标准：浮点数的"世界通用语"
2.1 标准诞生：从"巴别塔"到"普通话"
IEEE 754标准的诞生，本质上是为了解决早期浮点数格式混乱的问题。在没有标准的年代，每个硬件厂商都有自己的一套规则：有的用8位指数，有的用10位；有的尾数带符号，有的不带。这就导致同样的二进制数据，在不同机器上解读出的数值天差地别。
举个夸张的例子：某银行的转账系统在A服务器上计算"100.5元+200.3元"得出300.8元，但数据传到B服务器上，因为浮点数格式不同，被解读成了3008元——这要是真发生了，银行怕是要赔惨了。
IEEE 754标准就像给所有计算机厂商发了一本"浮点数字典"，规定了：
- 浮点数的存储格式（多少位存符号，多少位存指数，多少位存尾数）
- 指数的表示方法（用"偏移值"避免正负指数的麻烦）
- 特殊值的表示（比如无穷大、NaN）
- 运算规则（加减乘除时怎么处理精度）
有了这本"字典"，不管是Intel的CPU、AMD的芯片，还是Java、Python这些编程语言，处理浮点数都有了统一的依据。
2.2 单精度和双精度：精度与范围的权衡
IEEE 754标准里最常用的两种格式是单精度（float） 和双精度（double）。你可以简单理解成：单精度是"经济型"，用32位存储，适合对精度要求不高、需要节省内存的场景；双精度是"豪华型"，用64位存储，精度更高，范围更大，适合科学计算、金融等对精度敏感的场景。
2.2.1 单精度（32位）的结构
单精度浮点数把32位分成三部分：
- 符号位：就1位，0是正数，1是负数。比如3.14的符号位是0，-3.14是1。
- 指数位：8位，用"偏移值"表示指数。单精度的偏移值是127，所以实际指数 = 存储的指数值 - 127。比如存储的指数是128，实际指数就是1（128-127=1）。
- 尾数位：23位，默认前面有个"隐含的1"（即实际尾数是"1.xxxxxx"），这样能多表示一位精度。比如尾数位是100...000（23个0），实际尾数就是1.1（二进制）。
举个例子：用单精度表示1.5（十进制）。
- 1.5的二进制是1.1（整数部分1是1，小数部分0.5是1×2⁻¹=0.1）。
- 符号位：0（正数）。
- 指数：因为是1.1×2⁰，所以实际指数是0，存储的指数就是0+127=127（二进制01111111）。
- 尾数位：把1.1的整数部分1去掉，剩下的0.1用23位表示，就是10000000000000000000000（后面补22个0）。
完整的32位二进制就是：
0 01111111 10000000000000000000000。2.2.2 双精度（64位）的结构
双精度的结构跟单精度类似，只是位数更多：
- 符号位：同样1位，规则不变。
- 指数位：11位，偏移值是1023，所以实际指数 = 存储的指数值 - 1023。
- 尾数位：52位，同样隐含一个1，实际尾数是1.xxxxxx（52位二进制小数）。
还是用1.5举例子：
- 二进制还是1.1。
- 符号位：0。
- 指数：实际指数0，存储的指数是0+1023=1023（二进制01111111111）。
- 尾数位：去掉1后，0.1用52位表示，就是1000000000000000000000000000000000000000000000000000（补51个0）。
完整的64位二进制就是：
0 01111111111 1000000000000000000000000000000000000000000000000000。2.2.3 两者的区别在哪？
特性 | 单精度（float） | 双精度（double） |
总位数 | 32位 | 64位 |
指数位长度 | 8位 | 11位 |
尾数位长度 | 23位 | 52位 |
指数偏移值 | 127 | 1023 |
十进制有效数字 | 约7位 | 约15-17位 |
最大表示范围 | 约±3e38 | 约±1e308 |
简单说，双精度因为尾数位更多（52位 vs 23位），所以精度更高；指数位更多（11位 vs 8位），所以能表示的数值范围更大。
2.3 特殊值：当浮点数"无法表示"时
除了正常的数值，IEEE 754还规定了一些"特殊值"，用来表示那些"算不出来"或者"超出范围"的情况。
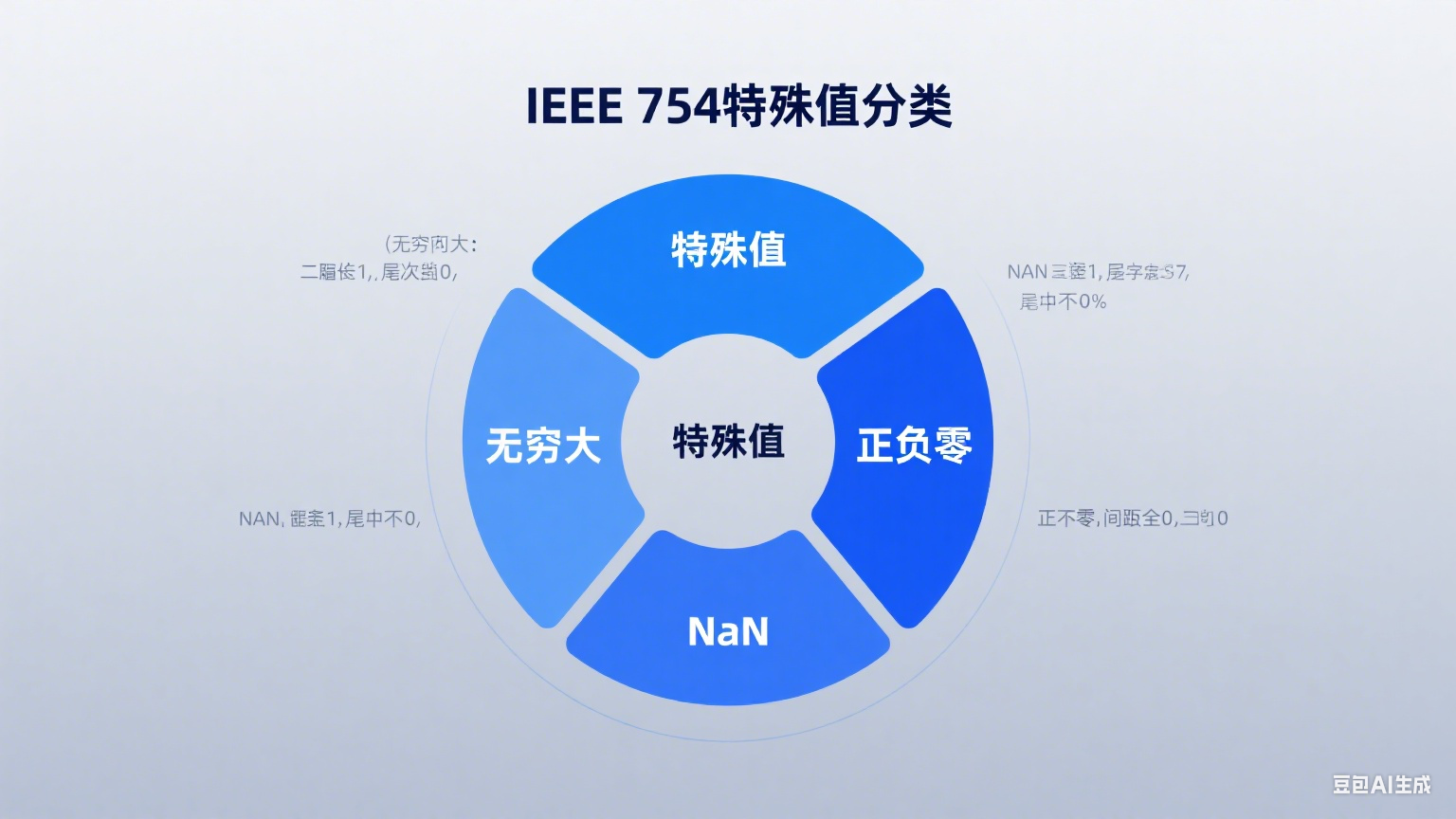
- 无穷大（Infinity）：当一个数大到超出浮点数能表示的最大范围时，就会显示无穷大。比如1e309用双精度表示就是+Infinity，-1e309就是-Infinity。在存储上，无穷大的指数位全是1，尾数位全是0，符号位0是正无穷，1是负无穷。
- NaN（Not a Number）：表示"不是一个数"，比如0除以0、负数开平方这些无意义的运算，结果都是NaN。NaN的指数位全是1，尾数位不全是0（只要有一位是1就行）。有意思的是，NaN不等于任何数，包括它自己——你在代码里写
NaN == NaN，结果是false。
- 零（0）：有+0和-0两种，符号位分别是0和1，指数位和尾数位全是0。在大多数情况下，+0和-0的效果一样，但在某些场景（比如除法）中会有区别，比如1/+0是+Infinity，1/-0是-Infinity。
三、十进制和二进制的"互译"：浮点数转换的核心步骤
知道了IEEE 754的格式，接下来咱们就得学怎么把十进制数转换成这种格式，以及怎么把二进制格式转回十进制。这就像学外语，既要会把中文翻译成英文，也要会把英文译回中文。
3.1 十进制转二进制：整数和小数"分家"处理
十进制转二进制浮点数，得把整数部分和小数部分拆开处理，最后再合并。
3.1.1 整数部分：除2取余，逆序排列
比如把十进制的13转换成二进制：
这个过程很好记：除2得商和余数，直到商为0，余数倒着写。
3.1.2 小数部分：乘2取整，顺序排列
再比如把0.625（十进制）转换成二进制：
这里要注意：有些小数可能永远乘不到0，比如0.1（十进制），转换成二进制是0.0001100110011...（循环），这也是为什么0.1+0.2会有误差——因为它们的二进制表示是无限循环的，浮点数只能存近似值。
3.1.3 合并成科学计数法
把整数和小数部分的二进制合并，再转换成"1.xxxx×2^指数"的形式（规格化）。
比如13.625（十进制）：
- 整数部分13→1101，小数部分0.625→0.101，合并后是1101.101（二进制）。
- 移动小数点，直到整数部分只有1位：1101.101 = 1.101101 × 2³（小数点向左移了3位）。
- 所以这里的指数是3，尾数是1.101101。
- 输入十进制数：如 13.625 等带小数的十进制数值
- 拆分整数和小数：将数值拆分为整数部分（如 13）和小数部分（如 0.625）
- 整数转二进制：通过「除 2 取余，逆序排列」得到整数二进制（如 13→1101）
- 小数转二进制：通过「乘 2 取整，顺序排列」得到小数二进制（如 0.625→0.101）
- 合并二进制数：组合整数和小数部分（如 1101.101）
- 转换科学计数法：标准化为 1.xxxx×2^指数 形式（如 1.101101×2³）
- 映射 IEEE 754 格式：按标准分配符号位、指数位（含偏移值）和尾数位（含隐含 1）
3.2 二进制转十进制：按IEEE 754格式"拆解"
如果拿到一个IEEE 754格式的二进制数，怎么转回十进制？以单精度的0x41A00000（十六进制，对应二进制0 10000010 10100000000000000000000）为例：
- 拆分成三部分：
- 符号位：0（正数）
- 指数位：10000010（二进制）→ 十进制130
- 尾数位：10100000000000000000000（23位）
- 计算指数：实际指数 = 存储的指数 - 偏移值 = 130 - 127 = 3。
- 计算尾数：尾数位是101000...000，加上隐含的1，就是1.101（二进制）。转换成十进制：1 + 1×2⁻¹ + 0×2⁻² + 1×2⁻³ = 1 + 0.5 + 0 + 0.125 = 1.625。
- 合并结果：数值 = (-1)^0 × 1.625 × 2³ = 1.625 × 8 = 13（十进制）。
是不是很简单？双精度的转换步骤一样，只是指数偏移值换成1023，尾数位更长而已。
3.3 手工转换容易踩的坑
- 忘记隐含的1：尾数位存储的是"1.xxxx"去掉1之后的部分，计算时一定要加回来，不然结果会差一倍。
- 指数计算错误：单精度偏移值是127，双精度是1023，千万别搞混。比如单精度指数位全1是255，实际指数是255-127=128，但这时候其实是特殊值（无穷大或NaN），正常指数范围是-126到+127。
- 小数部分无限循环：比如0.1的二进制是无限循环的，手工转换时可能会截断，导致误差——这也是为什么实际开发中很少手工转换，而是用代码或工具。
四、内存里的浮点数：字节序的"小陷阱"
浮点数在内存中是按位存储的，但不同系统存储这些位的顺序可能不一样，这就是"字节序"问题。别小看这个问题，跨平台传输数据时，字节序搞错了，数值可能会差十万八千里。
4.1 大端序和小端序：谁先谁后？
计算机内存是按"字节"（8位）划分的，32位浮点数需要4个字节，64位需要8个字节。问题来了：这几个字节是按什么顺序存在内存里的？
- 大端序（Big-Endian）：高位字节存在低地址，低位字节存在高地址。就像咱们写数字，从左到右是高位到低位（比如1234，1是高位，4是低位）。
- 小端序（Little-Endian）：低位字节存在低地址，高位字节存在高地址。跟大端序正好相反。
比如单精度浮点数0x41A00000（十六进制，对应十进制13），它的4个字节是0x41、0xA0、0x00、0x00。
存储方式 | 内存地址（低→高） | 存储内容 | 示意图 |
大端序 | 地址0 → 地址1 → 地址2 → 地址3 | 0x41 → 0xA0 → 0x00 → 0x00 | 高位在前，符合人类读写习惯 |
小端序 | 地址0 → 地址1 → 地址2 → 地址3 | 0x00 → 0x00 → 0xA0 → 0x41 | 低位在前，便于硬件处理 |
如果不处理字节序，小端序系统把数据发给大端序系统，对方会解读成0x0000A041，对应的浮点数完全是另一个数，这就乱套了。
4.2 跨平台怎么处理？
解决办法很简单：约定一个标准字节序。网络传输中通常用大端序（称为"网络字节序"），发送方先把自己的主机字节序转换成网络字节序，接收方再转回来。
在C/C++里，可以用
htonl（主机到网络长整数）、ntohl（网络到主机长整数）这类函数处理。Java更省心，因为JVM规定了浮点数的存储和传输都用大端序，不用开发者自己操心。比如你用Java的
DataOutputStream写一个float，它会自动按大端序写入；用DataInputStream读时，也会按大端序解析，不管运行在什么架构的CPU上。五、浮点数字节序转换流程
流程说明：
🖥️ 发送方：产生原始浮点数数据（使用主机字节序存储）
🔄 主机→网络字节序：通过转换函数（如htonl）将数据标准化为网络字节序（大端序）
📡 传输：通过网络协议或存储介质传递标准化数据
🖥️ 接收方：接收网络字节序格式的数据
🔄 网络→主机字节序：通过转换函数（如ntohl）将数据转回接收方的主机字节序
六、实际开发中的"老大难"问题：精度、性能和兼容性
了解了原理，咱们再聊聊实际开发中最容易遇到的问题。浮点数转换看着简单，但在高并发、高精度要求的场景下，坑可不少。
6.1 精度损失：为什么0.1+0.2≠0.3？
这可能是程序员最常遇到的浮点数问题了。咱们用前面学的转换知识分析一下：
在金融场景中，这个问题可能导致严重后果。比如计算利息时，每次结算差一点点，累积起来可能就是一笔不小的数目。
6.2 怎么解决精度问题？
- 用高精度库：比如Python的
decimal模块、Java的BigDecimal，可以指定小数位数，避免二进制转换误差。比如用decimal计算0.1+0.2，能得到精确的0.3。
- 转换为整数计算：在金融场景中，通常把金额转换成"分"来计算（比如1元=100分），这样所有运算都是整数，避免小数问题。
- 合理调整计算顺序：比如计算(a + b) + c时，如果a和b很小，b和c很大，先算b+c可能导致a被"吃掉"（因为浮点数精度有限），这时候调整顺序可能减少误差。
6.3 自己写代码怎么优化？
- 减少不必要的转换：比如日志打印时，避免把浮点数反复转换成字符串。
- 批量处理：把多个转换操作集中处理，利用缓存或预计算提升效率。
- 用高效库：比如Java可以用
FastDoubleParser替代原生方法，Python可以用cdecimal替代默认decimal。
6.4 跨平台兼容性：别让字节序"搞破坏"
前面聊过字节序的问题，在分布式系统中，这个问题更突出。比如一个系统部署在x86（小端序）和ARM（有的用大端序）服务器上，如果数据传输时不统一字节序，就会出现数值错乱。
解决办法：
- 传输时用标准格式：比如网络传输用大端序，存储用固定格式（如JSON、Protocol Buffers，这些格式会自动处理字节序）。
- 序列化/反序列化时处理：用Thrift、Protobuf等工具，它们会统一数据格式，避免字节序问题。
- 做好兼容性测试：在不同架构的机器上跑测试用例，确保浮点数转换结果一致。
七、总结：浮点数转换的"道"与"术"
浮点数转换看似是个小问题，实则涉及计算机底层原理、算法优化、跨平台兼容等多个维度。咱们从浮点数的基本概念出发，聊了IEEE 754标准的来龙去脉，拆解了单精度和双精度的结构，掌握了十进制与二进制的互转方法，也分析了实际开发中的精度、性能和兼容性问题。
核心要点可以总结为：
- 原理是基础：理解符号位、指数位、尾数位的作用，以及隐含1、偏移值这些设计巧思，才能看透浮点数的本质。
- 标准是规矩：IEEE 754标准让浮点数有了统一的"语言"，解决了早期的混乱问题。
- 实践有技巧：精度问题用高精度库，性能问题靠高效算法，兼容性问题注意字节序。
- 版本要跟上：像JDK这样的工具不断优化转换性能，升级版本往往能"躺赢"。
无论是科学计算、金融交易还是游戏开发，浮点数转换都无处不在。掌握这些知识，不仅能避开常见的"坑"，还能在性能优化时找到突破口。希望这篇文章能帮你真正搞懂浮点数转换，让你的代码更健壮、更高效！
参考资料
- 《IEEE 二进制浮点数算术标准（IEEE 754）》：
- 《计算机组成与设计：硬件/软件接口》：百度学术-计算机组成与设计。
- 《深入理解计算机系统》：百度学术-深入理解计算机系统。
- 《IEEE 754 (被广泛使用的浮点数运算标准)》：IEEE 754(被广泛使用的浮点数运算标准)_百科
- 作者:Honesty
- 链接:https://blog.hehouhui.cn/archives/ieee-754-floating-point-conversion-optimization-guide
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。